Herzlich willkommen,
Sich selbst etwas beibringen!
liebe Schülerinnen und Schüler des Q11-Physik-Kurses von BAU!
Auf dieser Seite erhaltet Ihr Aufträge, Materialien und Links zu den zu behandelnden Inhalten.
Zu behandelnde Inhalte
Bitte die roten Links anklicken, um den jeweiligen Eintrag ansehen zu können!
Wiederholung: Huygenssches Prinzip und Beugung (Ausklappen)
Sieh Dir die Seite "Interferenzphänomene" im Wikibook Physik Oberstufe an:
de.wikibooks.org/.../_Interferenzphänomene
Dort sind (u. a.) das Huygenssche Prinzip und die Entstehung von Kreis- bzw. Zylinder bzw. Kugelwellen schön erklärt. Man findet dort auch eine noch schönere Darstellung des Phänomens der Beugung am Einfachspalt als die folgende Darstellung:
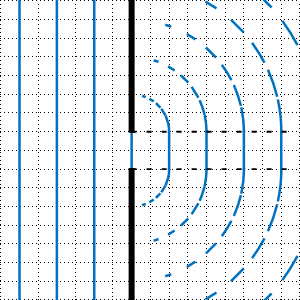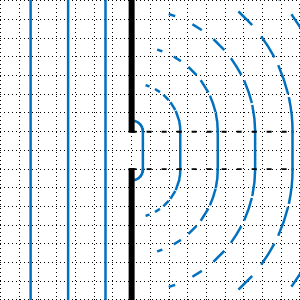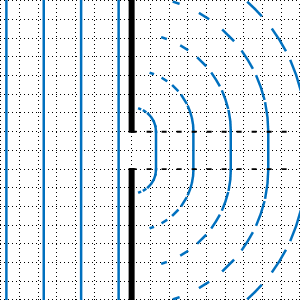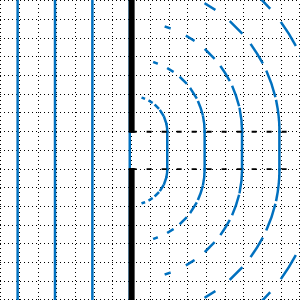
Materialien und Links usw.
Licht: Beugung und Interferenz am Einfachspalt und am Doppelspalt (Ausklappen)
Lade Dir die PDF-Datei herunter und sieh sie Dir genau an!
1. Beugung und Interferenz von Licht am Einfachspalt
Wenn man einen Laserstrahl auf einen schmalen Spalt auftreffen lässt, entsteht auf einem Schirm (d. h. auf der Wand in einiger Entfernung) ein Beugungsbild des Spaltes. Anstelle des punktförmigen "Laser-Points" sieht man eine Beugungsfigur von größerer Breite.
Für Interessierte: Warum bei der Beugung von Licht am Einfachspalt unter bestimmten Winkeln Minima auftreten (d. h. warum es zur Auslöschung durch Interferenz kommt, obwohl ja nur ein Spalt vohanden ist), wird im Wikibook Physik Oberstufe schön erklärt:
de.wikibooks.org/.../_Interferenzphänomene#Der_Einzelspalt.
Für den Winkel des Minimums k-ter Ordnung bei einem Spalt der Breite gilt:
|
ACHTUNG: Der Gangunterschied für die Minima beim Einfachspalt ist ein ganzzahliges Vielfaches der Wellenlänge , so wie der Gangunterschied für die Maxima beim Doppelspalt.
2. Interferenz von Licht am Doppelspalt
Das Phänomen ist wahrscheinlich aus Jgst. 10 noch in Erinnerung.
Neu ist vermutlich die Erklärung dafür, dass Maxima mancher Ordnungen gar nicht auftreten (→ PDF-Datei): Bei bestimmten Winkeln liegt bei jedem einzelnen der beiden Spalte ein Minimum vor (s. oben). Die beiden von den beiden Spalten ausgehenden Elementarwellen können sich deshalb bei diesen Winkeln nicht zu einem Maximum überlagern.
3. Bestimmung der Wellenlänge des roten Laser-Lichtes
→ PDF-Datei und Versuch mit Auswertung im Unterricht
4. "Kleinwinkel-Näherung"
→ PDF-Datei
Für kleine Winkel im Gradmaß gilt:
|
|
bzw. nur für kleine Winkel im Bogenmaß gilt auch:
|
Materialien und Links usw.
Ph11_023_Beugung_u_Interferenz_v_Licht.pdf
(ca. 432 kB)
Interferenz von Licht am optischen Gitter (Ausklappen)
Vom Mehrfach-Spalt zum optischen Gitter
Wie sich das Interferenz-Bild auf dem Schirm verändert, wenn man nicht nur 2, sondern 3 oder 4 oder noch mehr Spalte beleuchtet, werden wir uns bei entsprechenden Versuchen im Unterricht ansehen.
Eine größere Anzahl gleich weit voneinander entfernter Spalte ist ein optisches Gitter. Der Abstand zweier benachbarter Spalte wird als Gitterkonstante bezeichnet.
Ergebnis der Versuche:
| Mit zunehmender Anzahl an beleuchteten Spalten werden die Interferenzmaxima intensiver und schärfer. Die bei 3 und 4 Spalten noch gut erkennbaren Nebenmaxima spielen bei größer werdender Spalt-Anzahl eine immer geringer werdende Rolle, denn ihre Intensität wird immer geringer. |
Eine sehr schöne Simulation und eine gut verständliche Animation, wie sich das Interferenz-Bild bei wachsender Spalt-Anzahl verändert, findet sich bei LEIFIphysik:
Vielfachspalt und Gitter (LEIFIphysik).
Unbedingt ansehen!
Wellenlängen-Bestimmung mit optischem Gitter
Mit einem optischen Gitter guter Qualität (d. h. kleiner und gleichmäßiger Abstand benachbarter Spalte) lässt sich die Wellenlänge von Licht sehr genau bestimmen.
Für den Winkel , unter dem das (scharfe) Maximum k-ter Ordnung erscheint, gilt (wie beim Doppelspalt):
|
Der Winkel lässt sich sehr genau durch die Messung zweier Streckenlängen ermitteln:
: Abstand des Max. k-ter Ord. vom Max. 0. Ord. auf dem Schirm
: Abstand "optisches Gitter - Schirm"
Es gilt (siehe auch: entsprechende Abbildung in der PDF-Datei "Beugung und Interferenz von Licht"):
|
Zusammen ergibt sich:
|
|
Materialien und Links usw.
Spektrum elektromagnetsicher Wellen (Ausklappen)
Elektromagnetisches Spektrum
Aus den vorherigen Jahrgangsstufen dürfte Dir bekannt sein:
An das Spektrum des sichtbaren Lichts (Wellenlänge von 390 nm bis 780 nm) schließen sich für unser Auge nicht sichtbare Bereiche elektromagnetischer Strahlung an:

- an der langwelligen Grenze (d. h. bei "Rot"):
Infrarot-Strahlung (IR) mit - an der kurzwelligen Grenze (d. h. bei "Violett"):
Ultraviolett-Strahlung (UV) mit
Elektromagnetische Wellen mit noch größeren Wellenlängen als bei der IR-Strahlung werden als Mikrowellen und Radiowellen bezeichnet. Im kurzwelligen Bereich schließen sich an die UV-Strahlung die Röntgenstrahlung und die Gammastrahlung an.
Eine schöne Übersicht über das Spektrum elektromagnetischer Strahlung gibt es auf Wikipedia:
Elektromagnetisches Spektrum (Wikipedia)
Aber auch die Darstellung in unserem Schulbuch auf den Seiten 176 und 177 enthält interessante Informationen.
Empfehlung: Einfach mal beides mit (bzw. bei) Interesse ansehen!
Materialien und Links usw.
Rundfunk als Anwendung el.-magn. Wellen (Ausklappen)
Funktionsprizip des Rundfunks
Als Beispiel für eine wichtige Anwendung el.-magn. Wellen betrachten wir das Prinzip der Informationsübertragung durch Rundfunk (hier: Amplitudenmodulation "AM"; heute wichtiger: Frequenzmodulation "FM").
Lade Dir die PDF-Datei herunter und sieh sie Dir an!
Lies Dir auch im Buch die Seiten 179 und 180 durch.
Materialien und Links usw.
Ph11_024_Rundfunk.pdf
(ca. 215 kB)
Abituraufgaben zur Interferenz von Licht (Ausklappen)
In den letzten Jahren gab es häufig in der Physik-Abiturprüfung Aufgaben zur Interferenz von Licht.
Alle, die Physik in Q12 belegen möchten, aber vor allem alle, die Physik als Abiturfach wählen möchten, sollen sich bitte mit den folgenden Abituraufgaben beschäftigen:
- Physik-Abitur 2015: 11-1 Aufgabe 3
- Physik-Abitur 2016: 11-1 Aufgabe 2
Dies Aufgaben waren eigentlich recht gut zu bearbeiten.
Materialien und Links usw.
Ph_Abi_2015_11-1-3.pdf
(ca. 164 kB)
Ph_Abi_2016_11-1-2.pdf
(ca. 201 kB)
Wdh. und Nachtrag: Wellenlängen-Bestimmung mit Hilfe einer stehenden Welle (Ausklappen)
1. Arbeitsblatt "Wellencharakter der Dipolstrahlung"
(Seite 1 der PDF-Datei)
- Elektrische Feldstärke , magnetische Flussdichte und Ausbreitungsrichtung :
Die beiden Momentbilder längs eines Wellenstrahls (links auf Seite 1 der PDF-Datei) zeigen:
und - Empfang elektromagnetischer Wellen
(→ links unten und rechts oben auf Seite 1 der PDF-Datei) - Ausbildung einer stehenden Welle
bei senkrechtem Auftreffen der Dipolstrahlung auf eine reflektierende Wand (z. B. auf eine Metallplatte)
2. Bestimmung der Wellenlänge mit Hilfe der stehenden Welle
(Seite 2 der PDF-Datei)
Wir untersuchen die von einem schwingenden Dipol ausgehende Strahlung genauer. Dazu verwenden wir einen sog. Mikrowellen-Sender. Die vom Sender ausgehende Strahlung trifft senkrecht auf die Metallplatte und wird reflektiert. Im Bereich zwischen Sender und Metallplatte bildet sich eine stehende Welle aus.
Die vom Sender ausgehende (nach rechts laufende) Welle überlagert sich mit der von der Metallplatte reflektierten (nach links laufenden) Welle.
Mit einem Empfangsdipol lassen sich zwischen Sender und Metallplatte Wellenknoten und Wellenbäuche feststellen. Der Abstand zweier benachbarter Wellenknoten entspricht einer halben Wellenlänge: .
Durch die Messung dieses Abstandes (aus Gründen besserer Genauigkeit: Messung von ) lässt sich die Wellenlänge der vom Mikrowellen-Sender ausgehenden Strahlung bestimmen.
3. Weitere Eigenschaften von (el.-magn.) Wellen
(Seite 3 der PDF-Datei)
- Reflexion (nach dem Reflexionsgesetz, z. B. an einer Metallplatte)
- Brechung (nach dem Brechungsgesetz)
- Beugung (demnächst)
- Interferenz (demnächst)
- Polarisation (→ Versuche)
Siehe auch (zu allem): Buch S. 162-163!
Materialien und Links usw.
Ph11_020_Dipolstrahlung_el_magn_Welle.pdf
(ca. 909 kB)
Beugung von Wellen (Ausklappen)
Wir rufen uns das in Jgst. 10 (hoffentlich) kennengelernte Phänomen der Beugung von Wellen in Erinnerung:
Eine Welle breitet sich beim Auftreffen auf eine Hindernis auch in den Schattenraum hinter dem Hindernis aus.
Experimentell erfahren wir dieses Phänomen beim Auftreffen der Dipolstrahlung des Mikrowellensenders auf einen Spalt: Auch an Stellen hinter dem Spalt, zu denen es vom Sender keine direkte Verbindung gibt, lässt sich mit dem Empfangsdipol Strahlung nachweisen: Die Mikrowellen-Strahlung wird also am Spalt gebeugt (in den Schattenraum hinein).
Materialien und Links usw.
Ph11_021_Beugung_von_Dipolstrahlung.pdf
(ca. 80 kB)
Huygenssches Prinzip und Interferenz von Wellen (Ausklappen)
Huygenssches Prizip
Jeder Punkt einer Wellenfront ist Ausgangspunkt (Zentrum) einer kreis- (2D) oder kugel- (3D) förmigen Elementarwelle. Die Elementarwellen überlagern sich. Ihre „Einhüllende“ bildet die neue Wellenfront.
Siehe auch: Buch S. 164-165
Interferenz von Wellen
Diese Inhalte sind besonders wichtig!
- Interferenz am Doppelspalt
- Gangunterschied Δs (Definition)
- Bedingungen für Maxima bzw. Minima
- Gangunterschied in großer Entfernung
- Bestimmung der Wellenlänge der Strahlung des Mikrowellensenders mit Hilfe des Doppelspalt-Versuchs
- Ausbreitungsgeschwindigkeit elektromagnetischer Wellen
Materialien und Links usw.
Ph11_022_Interferenz_von_Dipolstrahlung.pdf
(ca. 184 kB)
Abituraufgaben zur Interferenz von Dipolstrahlung (Ausklappen)
In den letzten Jahren gab es häufig in der Physik-Abiturprüfung Aufgaben zur Dipolstrahlung und insbesondere zur Interferenz von Dipolstrahlung.
Alle, die Physik in Q12 belegen möchten, aber vor allem alle, die Physik als Abiturfach wählen möchten, sollen sich bitte mit den folgenden Abituraufgaben beschäftigen:
- Physik-Abitur 2019: 11-2 Aufgabe 1
- Physik-Abitur 2013: 11-2 Aufgabe 3
Das waren im Großen und Ganzen eher dankbare Aufgaben(-teile).
Materialien und Links usw.
Ph_Abi_2019_11-2-1.pdf
(ca. 307 kB)
Ph_Abi_2013_11-2-3.pdf
(ca. 197 kB)
Elektrische und magnetische Wechselfelder (Ausklappen)
Die Versuche zur Abstrahlung eines Sendedipols, wodurch ein Lämpchen in der Mitte eines dazu parallel stehenden Empfangsdipols (gleicher Länge) auch über eine größere Entferung zum Leuchten gebracht werden kann, zeigen uns, dass der Sendedipol Strahlung aussendet, die weit in den Raum hineinreicht. Der Grund dafür ist (vereinfacht):
| Ein elektrisches Wechselfeld erzeugt ein magnetisches Wechselfeld. Ein magnetisches Wechselfeld erzeugt ein elektrisches Wechselfeld. |
Materialien und Links usw.
Buch S. 156-157
Stromstärke- und Spannungsverteilung längs des Dipols (Ausklappen)
Mit einem Empfangsdipol, in dem mehrere Lämpchen eingebaut sind, untersuchen wir den Verlauf der el. Stromstärke längs eines zum Schwingen angeregten Dipols. Mit einer Glimmlampe fahren wir entlang eines zum Schwingen angeregten Dipols und untersuchen damit den Verlauf der el. Spannung längs des Dipols.
In zeitlichen Abständen von T/4 veranschaulichen wir uns auch die jeweils vorhandenen elektrischen und magnetischen Felder in der unmittelbaren Umgebung des Dipols während einer vollen Schwingungsdauer T.
Materialien und Links usw.
Ph11_018_Dipol_Stromstaerke_Spannung.pdf
(ca. 133 kB)
Deutung der Dipol-Schwingung als stehende Welle (Ausklappen)
Der Verlauf der Stromstärke längs des schwingenden Dipols (aber auch der Verlauf der Spannung) lässt uns die Dipolschwingung als stehende Welle deuten. Daraus ergibt sich der folgende Zusammenhang zwischen der Länge des Dipols und der Wellenlänge der stehenden Welle:
|
|
bzw. |
|
Mit dem Zusammenhang, dass die Ausbreitungsgeschwindigkeit jeder Welle gleich dem Produkt aus ihrer Wellenlänge und ihrer Frequenz ist,
|
ergibt sich für die Frequenz der Grundschwingung eines Dipols:
|
|
Dieser Inhalt ist auch besonders wichtig!
Mit diesen Zusammenhängen lässt sich bestimmen, mit welcher Frequenz ein Dipol mit einer bestimmten Länge optimal zum Schwingen angeregt werden kann bzw. welche Länge ein Dipol haben muss, damit er mit einer bestimmten Anregungsfrequenz optimal abstrahlen kann.
(→ PDF-Datei Seite 1 unten und Seite 2 oben)
Buch S. 184/17 "Sende- und Empfangsdipol"
Versuche bitte, diese Aufgabe zunächst selbst zu bearbeiten! Sieh Dir dann erst die Lösung auf S. 2 der PDF-Datei an.
Wiederholung aus Jgst. 10: Entstehung einer stehenden Welle
Unten auf Seite 2 der PDF-Datei sowie auf Seite 3 wird verständlich, wie eine stehende Welle entsteht als Überlagerung zweier gleichfrequenter, gegeneinander laufender Wellen.
Insbesondere entstehen bei der Ausbildung einer stehenden Welle:
- Wellenknoten:
Stellen, an denen die Amplitude zu jedem Zeitpunkt 0 ist, sowie - Wellenbäuche:
Stellen, an denen die Amplitude der Schwingung maximal ist.
Materialien und Links usw.
Ph11_019_Dipol_stehende_Welle.pdf
(ca. 836 kB)
Dipolstrahlung als elektromagnetische Welle (Ausklappen)
1. Arbeitsblatt "Wellencharakter der Dipolstrahlung"
(Seite 1 der PDF-Datei)
- Elektrische Feldstärke , magnetische Flussdichte und Ausbreitungsrichtung :
Die beiden Momentbilder längs eines Wellenstrahls (links auf Seite 1 der PDF-Datei) zeigen:
und - Empfang elektromagnetischer Wellen
(→ links unten und rechts oben auf Seite 1 der PDF-Datei) - Ausbildung einer stehenden Welle
bei senkrechtem Auftreffen der Dipolstrahlung auf eine reflektierende Wand (z. B. auf eine Metallplatte)
2. Bestimmung der Wellenlänge mit Hilfe der stehenden Welle
(Seite 2 der PDF-Datei)
Wir untersuchen die von einem schwingenden Dipol ausgehende Strahlung genauer. Dazu verwenden wir einen sog. Mikrowellen-Sender. Die vom Sender ausgehende Strahlung trifft senkrecht auf die Metallplatte und wird reflektiert. Im Bereich zwischen Sender und Metallplatte bildet sich eine stehende Welle aus.
Die vom Sender ausgehende (nach rechts laufende) Welle überlagert sich mit der von der Metallplatte reflektierten (nach links laufenden) Welle.
Mit einem Empfangsdipol lassen sich zwischen Sender und Metallplatte Wellenknoten und Wellenbäuche feststellen. Der Abstand zweier benachbarter Wellenknoten entspricht einer halben Wellenlänge: .
Durch die Messung dieses Abstandes (aus Gründen besserer Genauigkeit: Messung von ) lässt sich die Wellenlänge der vom Mikrowellen-Sender ausgehenden Strahlung bestimmen.
3. Weitere Eigenschaften von (el.-magn.) Wellen
(Seite 3 der PDF-Datei)
- Reflexion (nach dem Reflexionsgesetz, z. B. an einer Metallplatte)
- Brechung (nach dem Brechungsgesetz)
- Beugung (demnächst)
- Interferenz (demnächst)
- Polarisation (→ Versuche)
Siehe auch (zu allem): Buch S. 162-163!
Materialien und Links usw.
Ph11_020_Dipolstrahlung_el_magn_Welle.pdf
(ca. 909 kB)
13.05. und 14.05.2020 sowie
20.05. (und 21.05. - Feiertag): Offener Schwingkreis - Hertzscher Dipol
Aufträge
Wir kommen zum letzten großen Abschnitt:
ELEKTROMAGENTISCHE SCHWINGUNGEN UND WELLEN
Elektromagnetische Wellen
Hefteintrag "Offener Schwingkreis - Hertzscher Dipol"
Lade Dir die PDF-Datei mit dem Hefteintrag herunter (rechts bzw. unten) und schreibe ihn ab.
Die zugehörigen Experimente wirst Du im Live-Unterricht zu sehen bekommen. Damit wir dafür ausreichend Zeit haben, wäre es schön, wenn Du den Hefteintrag am besten schon vor den Live-Unterrichtsstunden in Dein Heft übernehmen würdest.
Materialien und Links usw.
Ph11_017_El_magn_Dipol.pdf
(ca. 658 kB)
07.05.2020: Erzeugung ungedämpfter el.-magn. Schwinungen
Aufträge
Hefteintrag "Erzeugung ungedämpfter el.-magn. Schwingungen"
Lade Dir die PDF-Datei mit dem Hefteintrag herunter (rechts bzw. unten) und lies Dir den Hefteintrag einmal durch.
Sieh Dir nun die drei Experiment-Videos an:
- "Manuelle" Energiezufuhr beim Schwingkreis (Wdh.)
- Ungedämpfte el.-magn. Schwingung (1 Hertz)
- Ungedämpfte el.-magn. Schwingung (Tonfrequenz)
Schreibe nun den Hefteintrag ab!
Materialien und Links usw.
Ph11_016_Erz_ungedaempfter_el_magn_Schw.pdf
(ca. 752 kB)
Experiment-Video (Wdh.): "Energiezufuhr beim Schwingkreis"
(ca. 11,7 MB)
Experiment-Video: "Ungedämpfte Schwingung (1 Hertz)"
(ca. 19,3 MB)
Experiment-Video: "Ungedämpfte Schwingung (Tonfrequenz)"
(ca. 18,4 MB)
06.05.2020: Gedämpfte und ungedämpfte el.-magn. Schwinung
Aufträge
Experimente zum Schwingkreis
Sieh Dir die drei Experiment-Videos an:
- Entladung eines Kondensators über einen Widerstand
(Nachtrag zum 22.04.2020) - Entladung eines Kondensators über eine Spule
(Nachtrag zum 23.04.2020) - "Manuelle" Energiezufuhr beim Schwingkreis
Morgen gibt's dann die Fortsetzung:
"Automatische" Energiezufuhr beim Schwingkreis
(mit zugehörigem Hefteintrag)
Materialien und Links usw.
Experiment-Video: "Entladung Kondensator über Widerstand"
(ca. 17,7 MB)
Experiment-Video: "Entladung Kondensator über Spule"
(ca. 12,6 MB)
Experiment-Video: "Energiezufuhr beim Schwingkreis"
(ca. 11,7 MB)
30.04.2020: Übungen zur Thomsongleichung und zum el.-magn. Schwingkreises
Aufträge
(veröffentlicht am 01.05.2020)
Hefteintrag "Übungen zur Thomsongleichung"
Lade Dir die PDF-Datei mit dem Hefteintrag herunter (rechts bzw. unten).
Sieh Dir nun zunächst das Erklärvideo "Schwingungsdauer aus Diagramm bestimmen" an.
Schreibe nun den zugehörigen Teil des Hefteintrags ab (→ Seite 2 der PDF-Datei, oben)!
Aufgabe:
- Bestimme nun auf dieselbe Weise möglichst genau die Schwingungsdauer T der el.-magn. Schwingung, die im unteren Diagramm dargestellt ist. Das Lineal hilft, eine geeignete Länge auf der t-Achse zu ermitteln. Beachte, dass der t-U-Schreiber im unteren Diagramm den Stift mit 50 mm/s nach rechts bewegt!
- Berechne zum Vergleich die theoretisch erwartete Schwingungsdauer !
- Schicke mir eine E-Mail mit Deinen Ergebnissen (im E-Mail-Text oder als Foto oder Scan als Anlage)!
Wenn Du überlegst, Physik als Abiturfach zu wählen, sieh Dir bitte auch die Abituraufgabe auf S. 3 der PDF-Datei an! Sie passt ideal zu den gerade behandelten Inhalten! Versuche, diese Aufgabe zunächst einmal selbst zu bearbeiten. Vergleiche Deine Ergebnisse dann mit der Lösung (→ Seite 4 der PDF-Datei).
Materialien und Links usw.
Ph11_015_Thomsongleichung_Uebungen.pdf
(ca. 967 kB)
Erklärvideo: "Schwingungsdauer aus Diagramm bestimmen"
(ca. 13,0 MB)
29.04.2020: Thomsongleichung für die Frequenz eines el.-magn. Schwingkreises
Aufträge
Hefteintrag "Vergeich 'Federpendel - Schwingkreis' → Thomsongleichung"
Lade Dir die PDF-Datei mit dem Hefteintrag herunter (rechts bzw. unten) und schreibe den Hefteintrag am besten ab.
Sieh Dir nun das Erklärvideo "El.-magn. Schwingung - Thomsongleichung" an.
Darin wird zunächst noch einmal erklärt, wie eine el.-magn. Schwinung in einem el.-magn. Schwingkreis zustande kommt.
Durch einen Vergleich der mechanischen Schwingung eines Federpendels mit der el.-magn. Schwingung eines Schwingkreises wird anschließend die Formel für
- die Schwingungsdauer T
bzw.(nicht in FS) - für die Frequenz f
(FS S. 29)
der Schwingung des Schwingkreises hergeleitet.
Materialien und Links usw.
Ph11_014_Thomsongleichung_Hefteintrag.pdf
(ca. 333 kB)
Erklärvideo: "El.-magn. Schwingung - Thomsongleichung"
(ca. 38,6 MB)
23.04.2020: Entladung eines Kondensators über eine Spule
Aufträge
(veröffentlicht am 24.04.2020)
Hefteintrag "Entladung eines Kondensators über eine Spule"
Lade Dir die PDF-Datei mit dem Hefteintrag herunter (rechts bzw. unten) und schreibe den Hefteintrag am besten ab (Fortsetzung vom 22.04.).
Die am Kondensator anliegende Spannung U wird beim Entladen über die Spule in Abhängigkeit von der Zeit t mit einem sog. t-U-Schreiber aufgezeichnet (→ Seite 1 der PDF-Datei): Es entsteht eine elektromagnetische Schwingung.
Warum beim Entladen des Kondensators eine (gedämpfte) elektromagnetische Schwinung entsteht, wird auf Seite 2 der PDF-Datei erklärt (nur diese Seite abschreiben).
Blatt "Spannungs- und Stromverlauf bei einer Schwingung"
Auf Seite 3 der PDF-Datei (v. a. rechte Seite) wird neben dem Verlauf der am Kondensator anliegenden Spannung U auch der Verlauf der Stärke I des durch die Spule fließenden Stromes betrachtet.
Außerdem wird in vier (bzw. fünf) Momentaufnahmen der Zustand des Schwingkreises, d. h. das Vorhandensein eines el. Feldes im Kondensator bzw. eines magn. Feldes in der Spule, betrachtet.
Es sind die Momentaufnahmen zu den Zeitpunkten t = 0, t = 1/4 T (Schwingungsdauer), t = 1/2 T, t = 3/4 T (und t = T).
Außerdem wird noch der analoge Verlauf der Schwingung eines Federpendels dargestellt.
Versuche bitte, insbesondere die Diagramme (U und I) und Darstellungen (Schwingkreis-Zustände sowie Federpendel-Zustände) zu verstehen! Wir benötigen diese Zusammenhänge, um nächste Woche die Formel für die Schwingungsdauer T des el.-magn. Schwingkreises "herleiten" zu können.
Materialien und Links usw.
Ph11_013_El_magn_Schwingkreis_Hefteintrag.pdf
(ca. 700 kB)
22.04.2020: Entladung eines Kondensators über einen Widerstand
Aufträge
Wir kommen zum (vor-)letzten großen Abschnitt:
ELEKTROMAGENTISCHE SCHWINGUNGEN UND WELLEN
Elektromagnetische Schwingungen
Hefteintrag "Entladung eines Kondensators über e. Widerstand"
Lade Dir die PDF-Datei mit dem Hefteintrag herunter (rechts bzw. unten) und schreibe den Hefteintrag am besten ab.
Der Kondensator ("Ladungsspeicher") wird zunächst aufgeladen (Schalterstellung 1) und anschließend über einen el. Widerstand entladen (Schalterstellung 2). Die am Kondensator anliegende Spannung U wird beim Entladen in Abhängigkeit von der Zeit t mit einem sog. t-U-Schreiber aufgezeichnet (→ Seite 2 der PDF-Datei).
Betrachte das t-U-Diagramm: Die am Kondensator anliegende Spannung U nimmt zunächst schnell ab und dann immer langsamer.
Eigentlich ist das "klar": Bei großer Spannung U des Kondensators fließt ein großer Strom durch den el. Widerstand. Die Ladung Q nimmt dadurch schnell ab. Wegen U = Q/C (folgt aus C = Q/U) nimmt dadurch auch die am
Kondensator anliegende Spannung U schnell ab. Bei geringerer Spannung (bzw. Ladung) fließt ein geringerer Strom
durch den el. Widerstand, so dass nun die Ladung Q langsamer abnimmt, ebenso die el. Spannung U.
Aus dem t-U-Diagramm ist auch ersichtlich, dass in gleichen Zeitintervallen Δt = T1/2 die Spannung jeweils auf den halben Wert sinkt. Das bedeutet, dass die el. Spannung bei der Entladung über den el. Widerstand exponentiell abnimmt.
Hefteintrag "Entladung eines Kondensators über eine Spule"
Wir ersetzen nun den el. Widerstand durch eine Spule und zeichnen nun den zeitlichen Verlauf der am Kondensator anliegenden Spannung U beim Entladen über die Spule auf.
(Das ist sehr spannend! Das t-U-Diagramm gibt's aber erst morgen, hehe.)
Du kannst Dir schon einmal überlegen (bzw. wiederholen), welche Bedeutung die Induktivität einer Spule hat (→ 01.04.). Nur dann lässt sich der sich hier ergebende zeitliche Verlauf der Spannung U verstehen.
Materialien und Links usw.
Ph11_012_Entladung_Kondensator_Widerstand.pdf
(ca. 341 kB)
02.04.2020: "Autozündung" und "Magnetische Energie"
Aufträge
Hefteintrag "Modellversuch zur Autozündung" und
Hefteintrag "Magnetische Energie des Spulenfeldes"
Lade Dir die PDF-Datei mit dem Hefteintrag herunter (rechts bzw. unten).
Den Modellversuch zur Autozündung werde ich Euch hoffentlich bald "live" zeigen können!
Es geht um Folgendes: Mit Hilfe des Phänomens der Selbstinduktion bei einer Spule kann eine Glimmlampe zum Leuchten
gebracht werden, obwohl die vorhandene Spannung nur 4,5 V groß ist, aber die sog. Zündspannung der Glimmlampe bei
über 100 V liegt. Konkret: Beim Öffnen des Schalters bricht das Magnetfeld der Spule zusammen, so dass die Änderung des magnetischen Flusses, ΔΦ, in einer sehr kurzen Zeitdauer Δt stattfindet. Dadurch wird
an den Enden der Spule (und mit diesen ist die Glimmlampe verbunden - parallel geschaltet) eine große Spannung induziert, sodass die Glimmlampe kurz aufleuchtet.
Dadurch wird auch verständlich, dass im Magnetfeld der Spule Energie gespeichert ist, denn diese Energie lässt ja die Glimmlampe (nach dem Öffnen des Schalters) aufleuchten:
| Magnetische Energie des Feldes einer Spule | Zum Vergleich: Elektrische Energie des Feldes eines Kondensators | |
| Emag = 1/2 ⋅ L ⋅ I2 | Eel = 1/2 ⋅ C ⋅ U2 |
Übungen:
S. 141/29 a) "Spule (und Widerstand)"
Bei dieser Aufgabe ist nur die Formel für Emag anzuwenden (und die Formel für die Induktivität L)
(Lösung im Hefteintrag unten).
Physik-Abitur 2013 - Aufgabengruppe 11-2 - Aufgabe 2
Lade Dir die PDF-Datei mit der Abitur-Aufgabe herunter (rechts bzw. unten) und bearbeite Aufgabe 2!
(Lösung vielleicht demächst hier. Oder im Unterricht?)
Materialien und Links usw.
Ph11_011_Magnetische_Energie_Herfteintrag.pdf
(ca. 440 kB)
Ph_Abi_2013-11-2.pdf
(ca. 200 kB)
Aufträge
Hefteintrag "Induktivität"
Lade Dir die PDF-Datei mit dem Hefteintrag herunter (rechts bzw. unten). Wenn Du die Möglichkeit dazu hast,
dann drucke Dir den Hefteintrag aus (zumindest die ersten beiden Seiten). So kannst Du gleichzeitig das Erklärvideo UND
das Arbeitsblatt ansehen.
Sieh Dir nun das Erklärvideo "Induktivität" an!
Was sollte "hängenbleiben"?
Die physikalische Größe Induktivität L einer Spule (allg.: eines Leiters) ist ein Maß dafür,
wie sehr eine Spule (ein Leiter) beim Einschalten den beginnenden Stromfluss hemmt (und beim Ausschalten den
Stromfluss aufrecht erhalten "möchte"):
| Induktivität L groß | ↔ | langsamer Anstieg der Stromstärke (beim Einschalten) |
| Induktivität L klein | ↔ | schneller Anstieg der Stromstärke (beim Einschalten) |
S. 140/21 "Induktivität und Selbstinduktionspannungsverlauf"
Diese Aufgabe passt ideal zum gerade Gelernten!
Bitte diese Aufgabe - wie immer - zunächst selbstständig (d. h. OHNE Lösung) bearbeiten,
dann eigene Lösung mit Online-Lösung (im Hefteintrag auf Seiten 3 und 4) vergleichen und zu verstehen versuchen!
Aufträge
Sieh Dir als Erstes das Experiment-Video "Selbstinduktion (Einführung)" an!
Arbeitsblatt "Selbstinduktion"
Lade Dir die PDF-Datei mit dem Arbeitsblatt herunter (rechts bzw. unten). Wenn Du die Möglichkeit dazu hast,
dann drucke Dir dieses Arbeitsblatt aus. So kannst Du gleichzeitig die folgenden Experiment-Videos UND
das Arbeitsblatt ansehen.
Genauere Untersuchung: "t-I-Diagramm"
Sieh Dir die beiden weiteren Experiment-Videos an!
Im ersten Video wird erklärt, wie der Grundversuch geändert wird, um den zeitlichen Verlauf der Stromstärke
in den beiden Zweigen (Spulenzweig und Widerstandszweig) aufnehmen zu können.
Das zweite Video zeigt den zeitlichen Verlauf der Stromstärke: zunächst in beiden Zweigen, dann nur im Widerstandszweig und schließlich nur im Spulenzweig.
S. 142/33 "Selbstinduktion-Experiment"
Diese Aufgabe passt ideal zum gerade Gelernten!
Bitte diese Aufgabe - wie immer - zunächst selbstständig (d. h. OHNE Lösung) bearbeiten,
dann eigene Lösung mit Online-Lösung (siehe rechts bzw. unten) vergleichen und zu verstehen versuchen!
Materialien und Links usw.
Experiment-Video: Selbstinduktion (Einführung)
(ca. 23,7 MB)
Ph11_008_Selbstinduktion_Einfuehrung.pdf
(ca. 610 kB)
Experiment-Video: Selbstinduktion (Überblick "t-I-Diagramm")
(ca. 6,2 MB)
Experiment-Video: Selbstinduktion (Aufnahme "t-I-Diagramm")
(ca. 42,0 MB)
Ph11_009_A142_33.pdf
(ca. 440 kB)
Aufträge
Wenn Du Sehnsucht nach Ph1 hast, kannst Du Dir das kurze Begrüßungsvideo (rechts bzw. unten) ansehen.
Hefteintrag "Lenzsche Regel"
Lade Dir zunächst die PDF-Datei mit dem Hefteintrag herunter (rechts bzw. unten).
Zum besseren Verständnis solltest Du Dir das zugehörige Erklärvideo ansehen.
Blatt "Versuche zur Lenzschen Regel"
Lade Dir zunächst diese PDF-Datei herunter (rechts bzw. unten).
Zum besseren Verständnis kannst Du Dir die beiden zugehörigen Videos ansehen.
Blatt "Aufgabe zur Lenzschen Regel"
Lade Dir zunächst diese PDF-Datei herunter (rechts bzw. unten).
Bitte diese Aufgabe - wie immer - zunächst selbstständig (d. h. OHNE Lösung) bearbeiten,
dann eigene Lösung mit Online-Lösung (bereits auf dem Blatt) vergleichen und zu verstehen versuchen!
Materialien und Links usw.
(ca. 1,8 MB)
Ph11_005_Lenzsche_Regel_Hefteintrag.pdf
(ca. 490 kB)
(ca. 10,6 MB)
Ph11_006_Lenzsche_Regel_Versuche_Blatt.pdf
(ca. 240 kB)
Video vom Experiment "Waltenhofen-Pendel"
(ca. 3,4 MB)
Video vom Experiment "Wirbelstrombremse"
(ca. 8,6 MB)
Ph11_007_Lenzsche_Regel_Aufgabe_mit_Loesung.pdf
(ca. 410 kB)
19.03.2020: Erzeugung sinusförmiger Wechselspannung
Aufträge
Blatt "Erzeugung sinusförmiger Wechselspannung"
Wenn Du S. 140/16 (siehe 18.03.2020) bearbeitet hast, wird es Dir nicht schwer fallen zu vestehen,
was auf dem Blatt (siehe rechts bzw. unten) zur Erzeugung sinusförmiger Wechselspannung ausgeführt wird.
S. 140/17 b) "Rotierende Spule"
Nun können wir auch Teilaufgabe b) von S. 140/17 bearbeiten.
Bitte diese Aufgabe - wie immer - zunächst selbstständig (d. h. OHNE Lösung) bearbeiten,
dann eigene Lösung mit Online-Lösung (siehe rechts bzw. unten) vergleichen und zu verstehen versuchen!
Materialien und Links usw.
Ph11_003_Erzeugung_sinusf_Wechselsp_Blatt.pdf
(ca. 530 kB)
Ph11_004_A140_17b.pdf
(ca. 390 kB)
Zur Veranschaulichung kannst Du Dir ein Video anschauen:
www.youtube.com/watch?v=a4pOJONgUe4
18.03.2020: Übungen zum Induktionsgesetz
Aufträge
S. 140/16 "Leiterschleife, auch gedreht"
Bitte diese Aufgabe zunächst selbstständig (d. h. OHNE Lösung) bearbeiten,
dann eigene Lösung mit Online-Lösung (siehe rechts bzw. unten) vergleichen und unbedingt zu verstehen versuchen!
(Diese Aufgabe ist wichtig für das nächste Thema.)
S. 140/17 a) "Spule, in und aus Magnetfeld geführt"
Bitte auch diese Aufgabe zunächst selbstständig (d. h. OHNE Lösung) bearbeiten,
dann eigene Lösung mit Online-Lösung (siehe rechts bzw. unten) vergleichen und zu verstehen versuchen!
Materialien und Links usw.
Ph11_001_A140_16.pdf
(PDF-Datei, ca. 800 kB)
Ph11_002_A140_17a.pdf
(PDF-Datei, ca. 400 kB)